Identidades trigonometricas

Una identidad trigonométrica es una igualdad entre expresiones que contienen funciones trigonométricas y es válida para todos los valores del ángulo en los que están definidas las funciones (y las operaciones aritméticas involucradas).
se define cos²α, sen²α, otros; tales que sen²α es (sen α)²

Relación seno coseno

cos² α + sen² α = 1

Relación secante tangente

sec² α = 1 + tg² α

Relación cosecante cotangente

cosec² α = 1 + cotg² α

Razones trigonometricas de la suma y diferencia de angulos

Ejem:

1)

       

2)

      

^{ESTAMOS EN MANTENIMIENTO, PRONTO HABRA MAS INFORMACION}

^GRACIAS

Grafico de funciones trigonometricas

La funcion seno

El seno de un número real t es la coordenada y (altura) del punto P en el siguiente diagrama, donde |t| es el largo del arco que se indica.

Grafica de la funcion seno

                    

Grados      Sen

0º              0

90º            1

180º          0

270º         -1

360º          0

Funcion seno general

La funcion seno generalizado tiene la siguiente forma:

y= Asen{w(x-a)}+c

• A es la amplitud (la altura de cada máximo arriba de la línea base).
• C es el desplazamiento vertical (la altura le la línea base).
• P es el periodo o longitud de onda (el longitud de casa ciclo).
• ω es la frecuencia angular, y se expresa por
          ω= 2π/P o P = 2π/ω.
• α es el desplazamiento de faso.

Funcion coseno

El coseno de un número real t es la coordenada x del punto P en el siguiente diagrama, donde |t| es el largo del arco que se indica.

cos t = coordenada x del punto P
sin t = coordenada y del punto P

Grafica función coseno  

y= cos x

Grados     Coseno

0º              1

90º            0

180          -1

270º          0

360º          1

Funcion coseno general

Triangulos Oblicuangulos

Un triángulo oblicuángulo es aquel que no es recto ninguno de sus ángulos, por lo que no se puede resolver directamente por el teorema de Pitágoras, el triángulo oblicuángulo se resuelve por leyes de senos y de cosenos, así como el que la suma de todos los ángulos internos de un triángulo suman 180 grados.

                            

Triangulo rectangulo

Sen A= a/c     a2= c2-b2    P=a+b+c     Ar= (b*a)/2

Cos A= b/c    b2= c2-a2

                      c2= a2+b2

A=25º    B=65º  C=90º  a=30  b=63.44  c=70  P=163  Ar=951

Sen25º = 30/c         Cos25º= b/70      P=a+b+c     Ar=(b*a)/2

c= 30/Sen25º          b= 70*Cos70º     P=163         Ar= 951

c= 70 R//                 b= 63.44 R//

                       

RESOLUCION DE TRIANGULOS RECTANGULOS

Se denomina al triángulo en el que uno de sus ángulos es recto, es decir, mide 90° (grados sexagesimales) ó π/2 radianes.

  

PITAGORAS:                                               a² = b² + b²

CIRCUNFERENCIA TRIGONOMETRICA

Es una circunferencia de radio uno, normalmente con su centro en el origen (0, 0) de un sistema de coordenadas cartesianas, de un plano euclídeo.

X²+Y²=1=RADIO=HIPOTENUSA

 

El seno es la razón entre el cateto opuesto y la hipotenusa.

 sen∞=co/hip

El coseno es la razón entre el cateto adyacente y la hipotenusa 

cos∞=ca/hip 

La tangente es la razón entre el cateto opuesto y el adyacente 

tan=co/ca


FUNCIONES DE LOS ANGULOS

SIGNOS DE LAS FUNCIONES

DEMOSTRACION  POR CUADRANTE

EJERCICIOS RESUELTOS

CONVERSION DE RADIAES-GRADOS Y VISCEVERSA
150°-----rad
150 x π /180=2.62 rad =5/6π rad.
180°=π
159°   x=2.63 rad =5/6π rad

INTRODUCCION
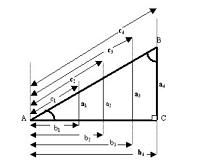
La trigonometría es una rama de la matemática, cuyo significado es "la medición de los triángulos".se encarga de estudiar las relaciones entre los ángulos y los lados de un triángulo.

A=b*h/2

P =L+L+L

ÁNGULOS

Es la abertura entre 2 rectas con un punto común llamado vértice Suelen medirse en unidades tales como el radian, el grado sexagesimal o el grado centesimal

 NOMENCLATURA

 

CLARIFICACIÓN:

POR SU ABERTURA 

Agudo:< 90°  

                       

Recto: = 90°                          

Obtuso:>90°                   

 

Llano: = 180°                        

 

POR SU POSICIÓN

Ángulos Consecutivos:son aquellos que tienen un mismo vértice y un lado en común.

 Ángulos Adyacentes:Estos ángulos son consecutivos y juntos forman un ángulo llano.

Ángulos opuestos por el vértice:Tienen el vértice en común y los lados en prolongación.

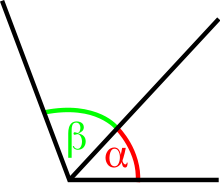
 Ángulos complementarios:Son aquellos que suman un ángulo recto. 

Ángulos suplementarios:Son los que suman un ángulo llano.

 ÁNGULOS FORMADOS POR 2 RECTAS PARALELAS CORTADAS POR UNA TRANSVERSAL

Ángulos correspondientes:Están al mismo lado de la transversal y corresponden a un externo e interno.(1 = 5,2 = 6,3 = 7,4 = 8)  

Opuestos por el vértice:1=4,2=3,5=8,6=7

Alternos Internos:Son internos y están al otro lado de la transversal(3=6,4=5)

Alternos Externos:Son externos y están al otro lado de la transversal(1=8,2=7)

Externos:Están fuera de las paralelas(1=2,7=8)

Internos:Están dentro de las paralelas(3,4,5,6)

Adyacentes Internos:1=7,2=8

Adyacentes Externos:4=6.3=5